Quadrants On A Coordinate Plane

What Is Quadrant?

In its essence, mathematics is the report of finding relationships. From planets to atoms; abstract to detailed, mathematics helps the states quantify everything. Information technology makes the states capable of understanding, analyzing, and predicting how all the known phenomena in our universe occur. And information technology's not like we utilise some advanced level science for this, we but use … graphs.

We graph the by and present of a phenomenon into simple figures and draw insights to predict future outcomes, and the branch of mathematics that makes this feat possible is known as Coordinate Geometry. Over the course of this article; our gameplay will be to empathise the well-nigh essential elements of coordinate geometry a.m.a The Coordinate Airplane and its Quadrants.

The Quadrants

In the cartesian system, the coordinate plane is divided into four equal parts by the intersection of the x-axis (the horizontal number line) and the y-centrality (the vertical number line).

These 4 regions are chosen quadrants because they each represent 1-quarter of the whole coordinate plane. They are denoted past Roman numerals and each of these quadrants have their own properties.

Quadrant I: The upper correct quadrant is the offset quadrant, denoted as Quadrant I. In this quadrant, the x-axis and the y-axis both accept positive numbers.

Quadrant II: The upper left quadrant is the second quadrant, denoted as Quadrant Ii. In this quadrant, the x-axis has negative numbers and the y-axis has positive numbers.

Quadrant Iii: The bottom left quadrant is the third quadrant, denoted as Quadrant III. In this quadrant, both the 10-axis and the y-axis have negative numbers.

Quadrant Four: The bottom right quadrant is the fourth quadrant, denoted as Quadrant IV. In this quadrant, the 10-centrality has positive numbers and the y-centrality has negative numbers.

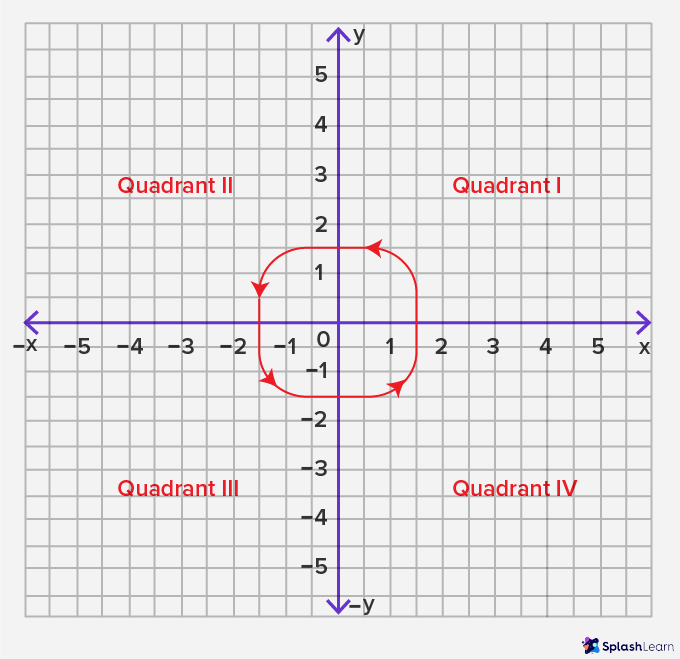
Annotation that the quadrants follow a counterclockwise club of naming.

Locating Points on the Quadrants

The coordinate plane is called two-dimensional considering anywhere on this plane where yous can put your finger, the location of that point volition need ii things: its altitude on the x-axis and its altitude on the y-axis.

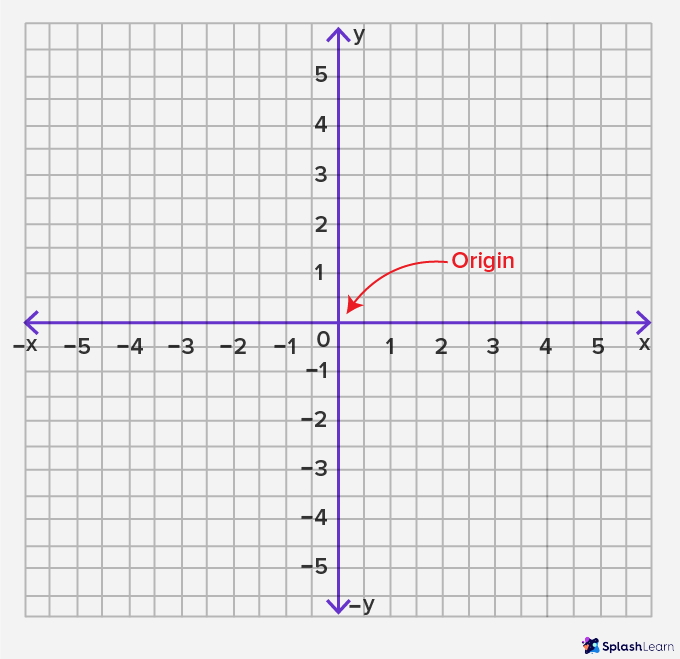
The left and the bottom role of the plane accept negative x-axis and negative y-centrality for negative integers. The point where the number lines intersect is called the origin.

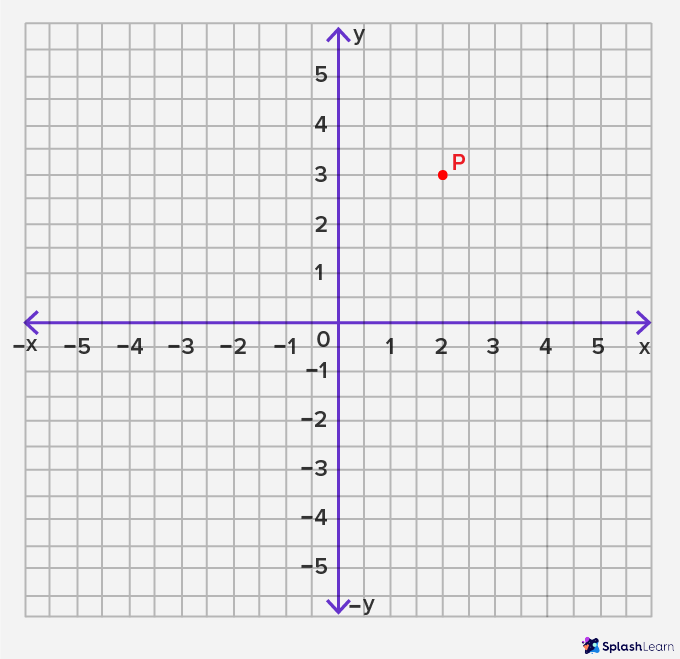
Let'southward see how the coordinate organisation works. We already know that any point on the coordinate plane has ii aspects: distance from the x-axis and distance from the y-axis. Let'southward await at this through an example. Permit's mark a random betoken on the plane and telephone call it "P".

Now start from this betoken and draw a directly line on the 10-axis and another straight line for the y-axis like this:

draw straight line from p point on x axis and y axis

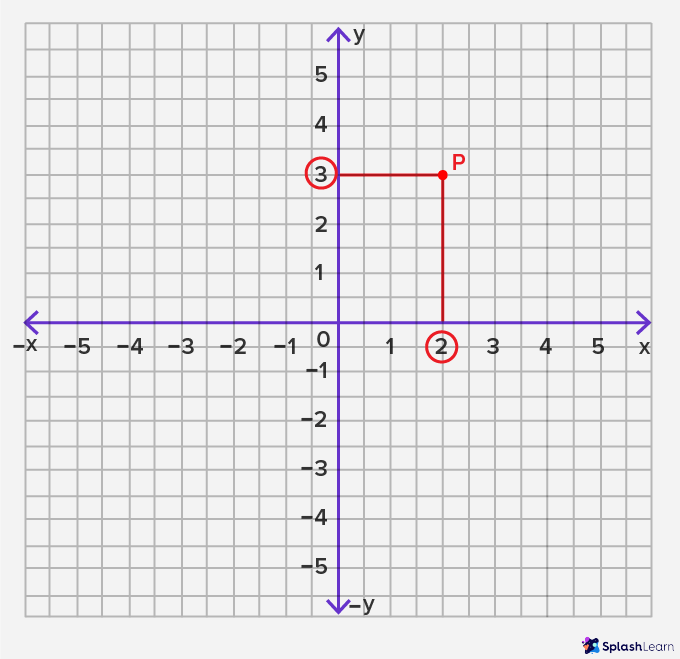
So the location of P on the x-axis is two units and the location of P on the y-axis is 3 units. Nosotros denote the location of the signal P as P(ii,3) where (2,3) is called an ordered pair that denotes the position of P.

set location of the point P called as ordered pair

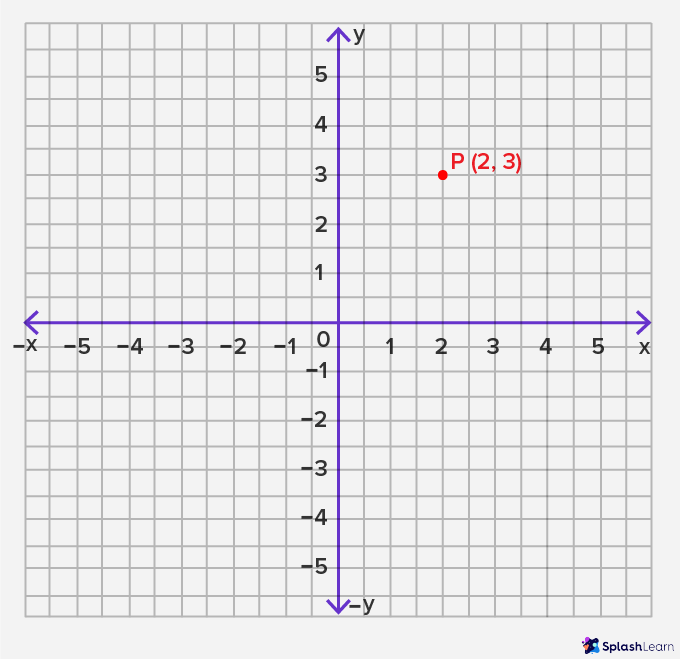
Every point on the coordinate aeroplane is in the form of the ordered pair (x,y), where ten and y are numbers that denote the position of the point with respect to the 10-axis and the y-axis respectively. The origin is denoted past (0,0).

Plotting Points

Let's say we want to plot the point A(4,-3) on the coordinate plane.

Past looking at this point, we can see that its x-coordinate is positive and y-coordinate is negative. So this betoken would lie in Quadrant IV.
To plot this point on the coordinate aeroplane, nosotros volition follow these steps:

Pace 1: Identify the x-coordinate of the given bespeak. In this case, it is 4.

Step 2: Start from the origin and move towards by iv units on the positive x-centrality.

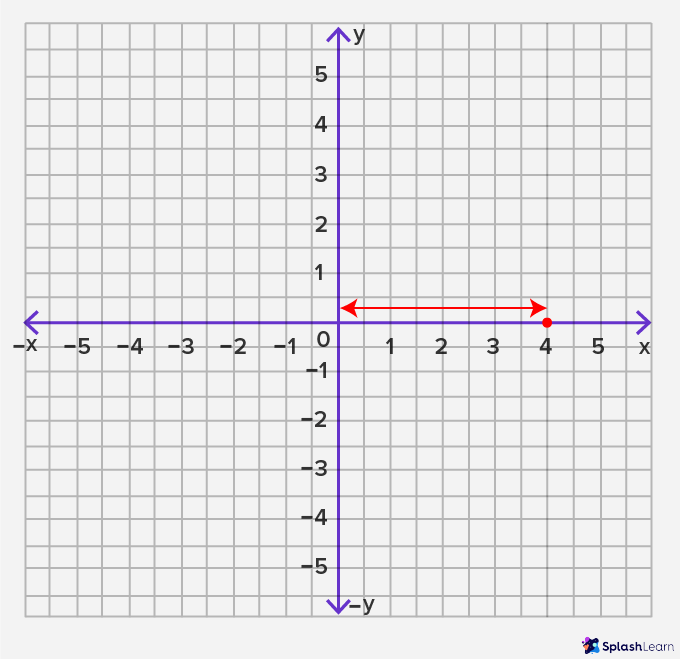
Step three: The y-coordinate in (4,-3) is -3, so nosotros volition beginning from this new point and move this point downward until it faces -iii on the negative y-axis.

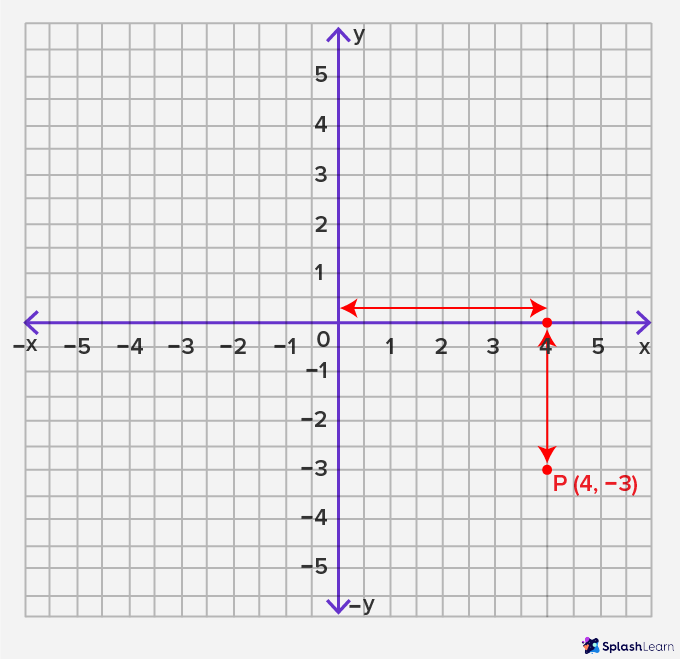
That's all we accept to do to plot a point on the coordinate plane.

Solved Examples

Example 1. Identify the quadrants in which each of the following points prevarication.

(i) (1,4)

(ii) (6,-3)

(three) (-4,-4)

(iv) (-1,8)

Answer:

(i) Quadrant I, because the x-coordinate and y-coordinate are both positive.

(2) Quadrant IV, because the x-coordinate is positive and y-coordinate is negative.

(iii) Quadrant Three, because the x-coordinate and y-coordinate are both negative.

(iv) Quadrant II, because the x-coordinate is negative and y-coordinate is positive.

Example ii. Give an instance of a bespeak that lies in Quadrant III.

Reply:

In Quadrant III, the coordinates of the 10-centrality and y-axis are both negative. (-i, -3) is an case of a point in this quadrant.

Example three. What quadrant is the origin in?

Ans:

The x-axis and the y-centrality intersect at the origin denoted by (0,0) since both these numbers are non-negative; the origin is said to be a part of Quadrant I.

Exercise Issues

Quadrant

Attend this Quiz & Test your knowledge.

three

four

five

Correct reply is: four
The coordinate airplane is divided into four equal parts by the intersection of the x-centrality and the y-axis and are called quadrants.

First Quadrant

Second Quadrant

3rd Quadrant

Quaternary Quadrant

Correct respond is: Start Quadrant
First Quadrant. Both the x-coordinate and y-coordinate are positive, therefore it lies in the outset quadrant.

(3,–5)

(6,2)

(–10,four)

(–ane,–8)

Correct answer is: (–1,–8)
(–i,–viii) since both x and y-coordinates are negative in the third quadrant.

Both positive

Both negative

x is positive, y is negative

x is negative, y is positive

Right reply is: x is positive, y is negative
x is positive and y is negative

Frequently Asked Questions

A quadrant is the region formed by the intersection of the x-axis and the y-axis on the coordinate plane.

What are the 4 quadrants?

The 4 quadrants are the regions formed by the intersection of the x-centrality and the y-axis on the coordinate plane. Their characteristic features are given as follows:

Quadrant I: Both x- and y-coordinates are positive.
Quadrant II: The 10-coordinate is negative and the y-coordinate is positive.
Quadrant 3: Both x- and y-coordinates are positive
Quadrant IV: The x-coordinate is positive and the y-coordinate is negative.

How do you lot name quadrants?

We commencement from the upper correct quadrant and marker that as Quadrant 50 and motion anticlockwise, marking each quadrant with Roman numerals: Quadrant ll, Quadrant lll, Quadrant IV.

Where practise the four quadrants meet?

The iv quadrants meet at the intersection of the x- and y-axis, called the origin. The origin is denoted by (0,0).